In the world of programming, the efficiency of algorithms plays a vital role in software development. The time complexity of an algorithm can determine how fast or slow a program can execute. The Big O notation comes into play here. Big O notation is a mathematical tool that helps in describing the efficiency of algorithms in terms of the input size.

What is Big O notation?

Big O notation is a mathematical concept used in computer science and programming to describe the complexity of algorithms. It is used to analyze the performance of an algorithm as the input size grows larger. In simple terms, Big O notation describes how much time and memory an algorithm needs to execute with respect to the size of its input.

The "Big O" in Big O notation stands for "order of" and represents the upper bound of the algorithm's time complexity. It helps programmers and software developers understand the scalability and efficiency of an algorithm in terms of time and space requirements.

How does Big O notation work?

Big O notation is based on the idea of asymptotic analysis. Asymptotic analysis involves analyzing an algorithm's behavior as the input size grows larger. The idea is to find a function that approximates the algorithm's time complexity for all input sizes.

The notation O(n) represents the upper bound of an algorithm's time complexity, where n is the input size. It is used to describe the worst-case scenario for an algorithm's execution time. For example, if an algorithm takes n^2 time to execute, its Big O notation would be O(n^2). This means that the algorithm's time complexity grows at a rate proportional to n^2.

Why is Big O notation important in programming?

Big O notation is an essential concept in programming because it helps developers understand the efficiency and scalability of algorithms. It provides a way to compare the performance of different algorithms and choose the best one for a specific task. Here are some of the reasons why Big O notation is crucial in programming.

1. Efficiency analysis: Big O notation helps developers analyze the time and space efficiency of algorithms. It allows them to compare the performance of different algorithms and select the best one for a particular task.
2. Optimization: By understanding the time complexity of an algorithm, developers can optimize it for better performance. They can identify the parts of the algorithm that are taking the most time and find ways to improve them.
3. Scalability: Big O notation provides a way to estimate the scalability of an algorithm. It helps developers understand how an algorithm will perform as the input size grows larger.
4. Algorithmic design: Big O notation plays a crucial role in algorithmic design. It helps developers choose the best algorithm for a specific task and design new algorithms that are more efficient.
5. Code readability: Big O notation helps developers write code that is more readable and easier to understand. By using standard notations, developers can communicate the time complexity of an algorithm more clearly.

Common Big O notations

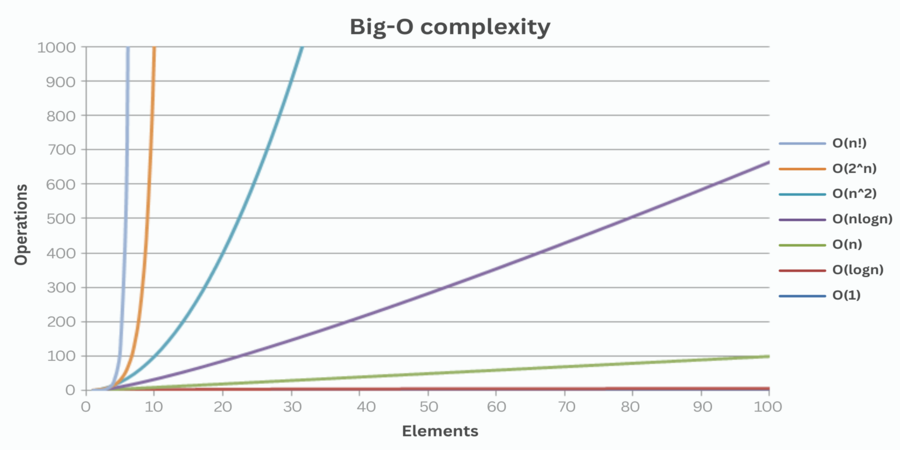
Here are some of the most common Big O notations and their corresponding time complexities:

1. O(1) - constant time complexity: An algorithm with constant time complexity takes the same amount of time to execute, regardless of the input size.
2. O(log n) - logarithmic time complexity: An algorithm with logarithmic time complexity takes less time to execute as the input size grows larger.
3. O(n) - linear time complexity: An algorithm with linear time complexity takes time proportional to the input size to execute.
4. O(n^2) - quadratic time complexity: An algorithm with quadratic time complexity takes time proportional to the square of the input size to execute.
5. O(2^n) - exponential time complexity: An algorithm with exponential time complexity takes an exponentially increasing amount of time to execute as the input size grows larger.
6. O(n log n) - linearithmic time complexity: An algorithm with linearithmic time complexity takes more time to execute than logarithmic time complexity but less time than quadratic time complexity.
7. O(n^3) - cubic time complexity: An algorithm with cubic time complexity takes time proportional to the cube of the input size to execute.

These are just a few examples of the many possible Big O notations. Each notation represents a different level of time complexity and scalability for algorithms.

Examples of Big O notation in action

Let's look at some examples of how Big O notation is used in programming.

Example 1: A function that finds the maximum element in an array.

This function takes O(n), where n is the number of items in the array. The algorithm iterates through the array once to find the maximum element. The time taken to execute the function will increase linearly as the size of the array grows larger.

Example 2: A function that sorts an array using bubble sort.

This function takes O(n^2), where n is the number of items in the array. The algorithm iterates through the array multiple times, comparing adjacent elements and swapping them if necessary. The time taken to execute the function will increase quadratically as the size of the array grows larger.

Example 3: A function that searches for an element in a binary search tree.

The time complexity of this function is O(log n), where n is the number of nodes in the binary search tree. The algorithm performs a binary search on the tree, dividing the search space in half at each step. The time taken to execute the function will increase logarithmically as the size of the tree grows larger.

Conclusion

Big O notation is an essential concept in programming that helps developers understand the efficiency and scalability of algorithms. It provides a way to compare the performance of different algorithms and choose the best one for a specific task. By understanding the time complexity of an algorithm, developers can optimize it for better performance, estimate its scalability, and design new algorithms that are more efficient. Big O notation is a powerful tool that every programmer should have in their arsenal.